Solid Primitives
(Available in TurbocAD Deluxe and TurbocAD Pro)
Primitives are simple shapes internally represented as linear or quadric geometry. The designer creates primitives from one of several choices, one point, two point, and by diagonals. Once created, each primitive is modified by a set of parameters unique for each type. Primitives supported by TurbocAD include spheres, blocks, cones, pyramids, prisms, tori, and slabs.

Sphere
A sphere is defined by a radius and origin. Three methods exist for creating spheres that include Sphere 1 Pt, Sphere 2 Pt, and Sphere Diagonals. The Snap tool registers the sphere center and points used by the designer to define the sphere.
Sphere One Point
The Sphere One Point method prompts the designer for the center location of the solid sphere. The designer defines the radius in a dialog box. One-point spheres are independent of the orientation of the construction plane.
Using the Sphere One Point tool
- Click a point defining the sphere center point.
- Use the Data Entry Fields to adjust the center or diameter.
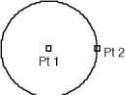
Sphere Two Point
Sphere Two Point creates a solid sphere from a center point and a point on the sphere extents. The distance from point 1 to point 2 defines the sphere radius.
Using the Sphere Two Point tool
- Click a point defining the sphere center point.
- Click a point defining the sphere radius point.
- Use the Data Entry Fields to adjust the center or dx, dy, dz distances to point 2.
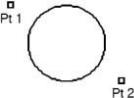
Sphere Diagonals
The Sphere Diagonals tool prompts the designer to specify a box by diagonals. The sphere center is positioned at the middle of the two points. The radius is calculated from the smallest length of the enclosing box.
Using the Sphere Diagonals tool
- Click a point defining the sphere upper left extents.
- Click a point defining the sphere lower right extents.
- Use the Data Entry Fields to adjust the center or dx, dy, dz distances to point 2.
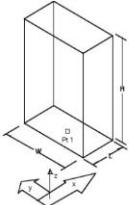
Blocks
The Block primitive is a rectangle whose mathematical definition is provided by width, height, and depth. Three methods are available for defining blocks that include 1 Pt, 2 Pt, and by diagonals. For all three methods, the construction plane is used to orientate the block.
Block One Point
The Block One Point method creates a block from one point supplied by the designer. The point provided is the base center. The designer supplies the length, width, and height in a dialog box. The orientation of the block is defined by the length, width, and height values along the x, y, and z axis of the construction plane.
Using the Block One Point tool
- Click one point for the block base center.
- Use the Data Entry Fields to adjust center, length, height, and width fields.
Block Two Points
The Block Two Points method creates a block whose height and z axis are defined by the two points supplied by the designer. The length and width are defined along vectors closest to the construction plane x and y axis.
Using the Block Two Points tool
- Click a center point.
- Click a point signifying the block height and z axis.
- Use the Data Entry Fields to adjust center, length, and width fields.
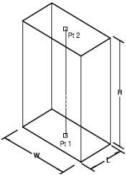
Block Diagonals
The Block by Diagonals method creates a block where point one is the block start, point 2 defines the length and width, and point 3 defines the block height.
Using the Block Diagonals tool
- Click base upper left point.
- Click base lower right point.
- Click a point along block height.
- Use the Data Entry Fields to adjust center, length, height, and width fields.
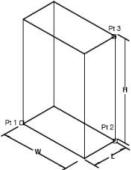
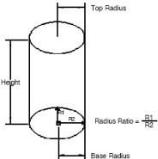
Cylinder
The Cylinder primitive is defined by a top and base radius, base radius ratio, and height. The base radius ratio defines the ratio between the major and minor radius. A base radius ratio of 1 is a circle. Values not equal to one yield elliptical cylinders.
Cylinder One Point
The Cylinder One Point method creates a cylinder from a point that is the center of the cylinder base. The orientation of the cylinder is determined by the z axis of the construction plane.
Using the Cylinder One Point tool
- Click cylinder base point.
- Use the Data Entry Fields to adjust the base center, height, and diameter.
Cylinder Two Point
The Cylinder Two Point method prompts the designer for the base center and top center. The orientation of the cylinder is determined by a vector from pt2 and pt1.
Using the Cylinder Two Points tool
- Click cylinder base point.
- Click cylinder height point.
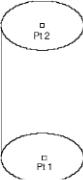
- Use the Data Entry Fields to adjust the base center, height, and diameter.
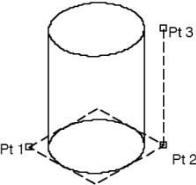
Cylinder Diagonals
The Cylinder Diagonals method creates a cylinder from three points. Point 1 and point 2 determine the base center extents. Point 3 determines the height. The cylinder may be elliptical.
Using the Cylinder Diagonals tool
- Click cylinder base lower left point.
- Click cylinder base lower right point.
- Click cylinder height point.
- Use the Data Entry Fields to adjust the center and height
Cone
The Cone primitive defines a solid with an elliptical base degenerating into a point. Three methods exist for creating cones:
One Point Defines a cone from its base center.
Two Points Defines cone axis and height.
Diagonals Define cone by box diagonals.
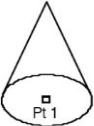
Cone One Point The Cone One Point prompts the designer to specify the cone base center.
Using the Cone One Point tool
- Click cone base center.
- Use the Data Entry Fields to adjust the center, diameter, and height attributes.
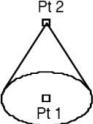
Cone Two Points
Cone Two Points creates a cone whose height axis is aligned with the given points. The height is extracted as the distance between the provided points.
Using the Cone Two Points tool
- Click cone base center.
- Click cone height.
- Use the Data Entry Fields to adjust the center, height, and diameter attributes.
Cone Diagonals
The Cone Diagonals method creates a cone from three points. Points 1 and 2 define a rectangle for an elliptical cone base. Point 3 is used to determine the height of the cone. If point 3 is in the plane of point 1 and 2, a default height for the cone is used. By holding the Shift key after locating point 1, you can force the rectangle to be square providing a radius ratio of 1 (a circular base).
Using the Cone Diagonals tool
- Click cone base lower left.
- Click cone base upper right.
- Click cone height point.
- Use the Data Entry Fields to adjust the center and height attributes.
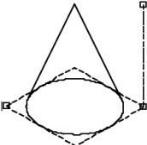
Torus
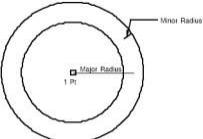
The Torus primitive is generated by revolving a circle about an axis. The torus is defined by an outer radius, inner radius, and center.
Torus One Point
The Torus One Point method prompts the user for the center point. The torus is aligned with the construction plane z axis.
Using the Torus One Point tool
- Click torus center point.
- Use the Data Entry Fields to adjust the major and minor radius values.
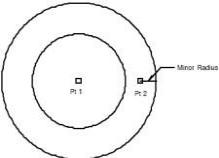
Torus Two points
The torus two-point method prompts the torus center and tube center. The designer specifies the radius value for the tube in the torus parameter dialog box.
Using the Torus Two Points tool
- Click torus center point.
- Click torus radius point.
- Use the Data Entry Fields to adjust the major and minor radius values.
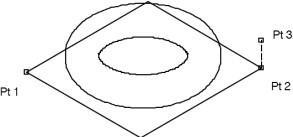
Torus Diagonals
The Torus Diagonals tool prompts the designer for three points. The first two points define a rectangle that locates the torus center and major radius length. The third point defines the radius of the tube (torus height).
Using the Torus Diagonals tool
- Click lower left point for torus base.
- Click upper right point for torus base.
- Click height point for torus minor radius.
Prism
The Prism primitive creates n-sided faced solids. The faces all form a 90-degree angle with the base.
Prisms are defined with a major and minor radii, centers, and heights.
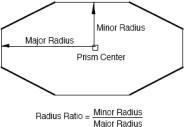
Prism Ratio Definition
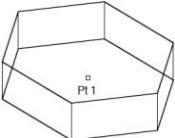
Prism One Point
The Prism One Point method prompts the designer for the prism base center. The height direction is taken from the z-axis of the current construction plane. The designer is prompted for additional radius values from the Prism dialog box.
Using the Prism One Point tool
- Click the prism base center.
- Use the Data Entry Fields to adjust the center, diameter, height, and number of sides attributes.
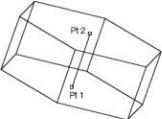
Prism Two Points
The Prism Two Point method creates a prism from two points defining the prism vertical axis. The designer is prompted for radius values with the Prism dialog box.
Using the Prism Two Points tool
- Click the prism base center.
- Click the prism height point.
- Use the Data Entry Fields to adjust the center, diameter, height, and number of sides attributes.
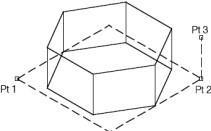
Prism Diagonals
The Prism Diagonals command creates a prism from three points. The first two points define a rectangle that specifies the prism’s radius and radius ratio. The third point defines the prism height.
Using the Prism Diagonals tool
- Click the first prism base corner.
- Click the second prism base corner.
- Click the prism height point.
Pyramid
A Pyramid contains n-sided flat faces sharing a common vertex tip. TurbocAD supports three methods for creating pyramids.
Pyramid One Point
A One Point Pyramid method prompts the designer for the pyramid center. The height and radius parameters are defined in a dialog box. The one-point pyramid is orientated along the construction plane z axis.
Using the Pyramid One Point tool
- Click the pyramid base center.
- Use the Data Entry Fields to adjust the pyramid height, diameter, and number of sides.
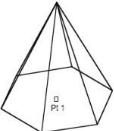
Pyramid Two Points
The Two Point Pyramid method prompts the user for two points that define the pyramid height and orientation.
Using the Pyramid Two Points tool
- Click the pyramid base center.
- Click the pyramid height center.
- Use the Data Entry Fields to adjust the pyramid height, diameter, and number of sides.
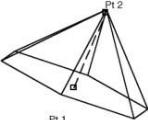
Pyramid Diagonals
The Pyramid Diagonals method prompts the designer for three points. The first two points define the length and width of the pyramid. The third point defines the pyramid height.
Using the Pyramid by Diagonals tool
- Click the pyramid lower left point.
- Click the pyramid lower right point.
- Click the pyramid height center.
- Use the Data Entry Fields to adjust the pyramid height, diameter, and number of sides.
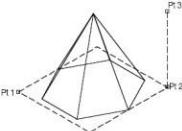
Ellipsoid
The last primitive in the tool palette is an Ellipsoid. Similar to a sphere, ellipsoids are extremely smooth and are useful as a foundation for some very interesting shapes. The Inspector supports modifying the three radius values for an ellipsoid.

Ellipsoid One Point
A One Point Ellipsoid method prompts the designer for the ellipsoid center and radius values for the x, y, and z axis.
Using the Ellipsoid One Point tool
- Click the Ellipsoid center.
- Use the Data Entry Fields to adjust the center and diameters along the x, y, and z axis.
Ellipsoid Two Points
The Two Point Ellipsoid method prompts the user for two points that define the ellipsoid major axis. Using the Ellipsoid Two Points tool
- Click the ellipsoid center.
- Click the ellipsoid major radius point.
- Use the Data Entry Fields to adjust the center, minor radius 1, and minor radius 2.
Ellipsoid Diagonals
The Ellipsoid Diagonals method prompts the designer for three points. The first two points define the length and width of the ellipsoid. The third point defines the ellipsoid height.
Using the Ellipsoid Diagonals tool
- Click the ellipsoid lower left point.
- Click the ellipsoid lower right point.
- Click the ellipsoid height.
- Use the Data Entry Fields to adjust the ellipsoid center, and three radius values.
Slab Primitive
A Slab is a collection of closed planar points that are extruded into a solid. If the points do not close, TurbocAD will automatically close them. The extrusion direction is determined by the order in which the points were entered. Clockwise points will produce a slab in the direction of the right-hand rule. Likewise, counterclockwise points will produce a slab in the opposite direction of the right-hand rule. Although points must be coplanar, they can be independent of the current construction plane.
Using the Slab Primitive tool
- Click on 3 or more planar points.
- Press the Esc key, double--click, enter key or right mouse button to terminate slab creation.
- Type in the height and optional draft using the Data Entry Fields.
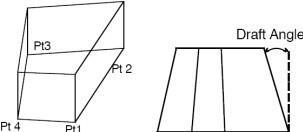
Slab Primitive Points and Draft Angle
Edit a Primitive Slab
Once a slab is created, you can later modify the slab height and draft angle. You can change the direction of the slab by specifying a negative value in the height field.
Paraboloid Primitive
The paraboloid primitive provides a means to create a quadric surface from one, two, or three point definitions. Use a paraboloid to create a reflectors/radars, automobile headlights, solar furnaces, antennas, and aerodynamic tips. The Paraboloid primitive is located in the solid primitives tool palette, last tool item. The one point paraboloid has a base center, and three radius values. The two point paraboloid has a base center, end.
The three point has two points defining the base diagonal, and one point defining the height. Each method provides a data entry window interface to change the associated radius values.
Paraboloid One Point
The Paraboloid One Point method creates a Paraboloid from one point supplied by the designer. The point provided is the base center. The designer supplies the R1, R2, and R3 in a dialog box.
Paraboloid Two Point
The Paraboloid two Point method creates a Paraboloid whose height and z axis are defined by the two points supplied by the designer.
Paraboloid Three Point
The Paraboloid three Point method creates a Paraboloid where point one is the Paraboloid start, point 2 defines the length and width and point 3 defines the Paraboloid height.